精度評価指標と回帰モデルの評価

この記事では、機械学習モデル作成後の評価方法について解説しています。機械学習自体の考え方や活用方法については、本サイトの別記事や外部のページを参考にしてください。

学会等、機械学習関連の研究発表の場で良く聞かれる言葉。

「R2が0.9と良好な値を示しており、良いモデルが作成できたといえます」
「RMSE は 1.3 であり、高い精度で予測できています」

本当に？？
一般的に回帰モデルの評価に用いられている精度評価指標ですが、その理論的なバックグラウンドを知らないと、利用方法を誤ってしまう場合があります。
本記事では機械学習で用いられる精度評価指標の背景および相互関係についてなるべく詳しく解説し、その活用方法の一案をお示しします。

数値を見る前に

はじめに、モデルの評価を行う上陥りやすい点をいくつか紹介します。

精度評価指標を用いてモデルの良し悪しを評価する上では、以下のようなことに注意を払う必要があります。

R², RMSE, MAE はいつでも比較できるわけではない！
全く同じデータに対して計算した場合のみ相対的な大小が比較可能で、異なるデータセット間での指標の比較は意味がありません。
モデル構築用データ、モデル検証用データ両方に対する精度を考慮する必要がある
そもそもモデル構築がうまくできていない場合、両データに対する精度がアンバランスになりがちです。
予測可能性には限界があることが多い
データに観測誤差(あるいは実験誤差)がある場合、精度指標の値には何らかの限界値が想定されます。例えば生理活性データ(Ki、IC50 等)は同じ系に対しても観測値がばらつくため、優秀すぎる精度指標の値は逆に信頼を得られません。
モデルには適用範囲がある
機械学習を用いて作成したモデルは、良くも悪くも使用したデータに左右されてしまいます。モデル検証用データに対する精度が高くても、外部データ(使用したデータから離れたデータ)を同じような精度で予測できるとは限りません。

回帰分析の精度評価指標

回帰分析とは、入力 \( X \) に対し出力 \( y \) が数値データとして得られる分析のことをいいます。(数値データ以外の出力としては、ラベル、順序尺度等が考えられます)
したがって、回帰分析の精度を評価するには、出力の実測値 \( y_{\mathrm{obs}} \) を出力の予測値 \( y_{\mathrm{pred}} \) がどの程度再現できているかを検討する必要があります。以下で紹介する精度評価指標も、\( y_{\mathrm{obs}} \) および \( y_{\mathrm{pred}} \) のベクトル \( \left( y_{\mathrm{obs}, i} \right) \) および \( \left( y_{\mathrm{pred}, i} \right) \) を用いて計算されます。

R² (決定係数)

R² (決定係数)は以下の式で計算され、\( \left( y_{\mathrm{obs}, i} \right) \) と \( \left( y_{\mathrm{pred}, i} \right) \) の間の相関係数を表します。ここで、\( \overline{y_{\mathrm{obs}}} \) は \( \left( y_{\mathrm{obs}, i} \right) \) の平均値を表します。

\[ R^2 = 1 - \frac{\sum_{i} (y_{\mathrm{obs}, i} - y_{\mathrm{pred}, i})^2}{\sum_{i} (y_{\mathrm{obs}, i} - \overline{y_{\mathrm{obs}}})^2} \]

python の機械学習ライブラリ scikit-learn[1] にも R² の計算関数 r2_score が実装されています。

from sklearn.metrics import r2_score

r2 = r2_score(y_obs, y_pred)

R² は \( \left( y_{\mathrm{obs}, i} \right) \) と \( \left( y_{\mathrm{pred}, i} \right) \) が完全に一致する場合に 1 となり、1 に近いほど精度の高い予測が行えていることを表します。

Root Mean Squared Error (RMSE)

RMSE は、後述する MAE と共に平均化された誤差の値を表します。

\[ RMSE = \sqrt{ \frac{ \sum_{i} (y_{\mathrm{obs}, i} - y_{\mathrm{pred}, i})^2 }{ n }} \]

ここで、n はサンプル数です。

scikit-learn 内には平方根を取る前の値である Mean Squared Error を計算する関数が実装されており、この関数を活用することで RMSE が計算されます。

import numpy as np
from sklearn.metrics import mean_squared_error

rmse = np.sqrt(mean_squared_error(y_obs, y_pred))

RMSE が 0 に近いほど見積もられる予測誤差が小さい、すなわち予測精度が高いことを表します。

また、RMSE と \( \left( y_{\mathrm{obs}, i} \right) \) の分散 \( \mathrm{VAR} \left( y_{\mathrm{obs}, i} \right) \) を用いて、R² は以下のように計算できます。

\[ R^2 = 1 - \frac{RMSE^2 \times n}{\mathrm{VAR} \left( y_{\mathrm{obs}, i} \right)} \]

Mean Absolute Error (MAE)

MAE は以下の式で計算され、RMSE と共に平均化された誤差の大きさを表します。

\[ MAE = \frac{ \sum_{i} | y_{\mathrm{obs}, i} - y_{\mathrm{pred}, i} | }{ n } \]

例によって scikit-learn には MAE を計算する関数が実装されています。いろいろと融通が効きやすいのでぜひ活用しましょう。

from skelearn.metrics import mean_absolute_error

mae = mean_absolute_error(y_obs, y_pred)

RMSE 同様、MAE も 0 に近いほど予測精度が高いことを表します。

RMSE、 MAE と最尤推定

RMSE と MAE は、どちらも最尤推定と密接に関係しています。

RMSE が最小となるのは、二乗誤差が最小となる時。すなわち、RMSE の最小化は最小二乗法と同値です。最小二乗法は、誤差の分布に正規分布を仮定した場合の最尤推定と一致します。

RMSE の最小化 = 二乗誤差の最小化 = 誤差に正規分布を仮定した場合の最尤推定

MAE が最小となるのは、絶対誤差が最小となる時。絶対誤差の最小化は、誤差の分布にラプラス分布を仮定した場合の最尤推定と一致します。

MAE の最小化 = 絶対誤差の最小化 = 誤差にラプラス分布を仮定した場合の最尤推定

一般にラプラス分布は正規分布よりも裾野が広く、多くの外れ値が観測されます。
多くの外れ値が存在するデータの誤差を評価したい、あるいは外れ値にあまり影響されない評価を行いたい場合、RMSE より MAE のほうが優れた指標であるといえるでしょう。
他方、基本的な線形回帰(MLR, PLS)から deep learning まで、最小化する関数には二乗誤差が使われていることも見逃せません。

まとめると、

	誤差関数	誤差分布	外れ値の影響
RMSE	二乗誤差	正規分布	大
MAE	絶対誤差	ラプラス分布	小

Observed-Predicted Plot (yyplot)

評価指標ではありませんが、回帰分析の良し悪しを評価する方法の一つに「Observed-Predicted Plot (yyplot)」があります。yyplot は、横軸に実測値(\( y_{\mathrm{obs}} \))、縦軸に予測値(\( y_{\mathrm{pred}} \))をプロットしたもので、プロットが対角線付近に多く存在すれば良い予測が行えています。

以下に yyplot の作成コード例、および乱数で作成したデータに対する実行例を示します。

import numpy as np
from matplotlib import pyplot as plt

# yyplot 作成関数
def yyplot(y_obs, y_pred):
    yvalues = np.concatenate([y_obs.flatten(), y_pred.flatten()])
    ymin, ymax, yrange = np.amin(yvalues), np.amax(yvalues), np.ptp(yvalues)
    fig = plt.figure(figsize=(8, 8))
    plt.scatter(y_obs, y_pred)
    plt.plot([ymin - yrange * 0.01, ymax + yrange * 0.01], [ymin - yrange * 0.01, ymax + yrange * 0.01])
    plt.xlim(ymin - yrange * 0.01, ymax + yrange * 0.01)
    plt.ylim(ymin - yrange * 0.01, ymax + yrange * 0.01)
    plt.xlabel('y_observed', fontsize=24)
    plt.ylabel('y_predicted', fontsize=24)
    plt.title('Observed-Predicted Plot', fontsize=24)
    plt.tick_params(labelsize=16)
    plt.show()

    return fig


# yyplot の実行例
np.random.seed(0)
y_obs = np.random.normal(size=(1000, 1))
y_pred = y_obs + np.random.normal(scale=0.3, size=(1000, 1))
fig = yyplot(y_obs, y_pred)

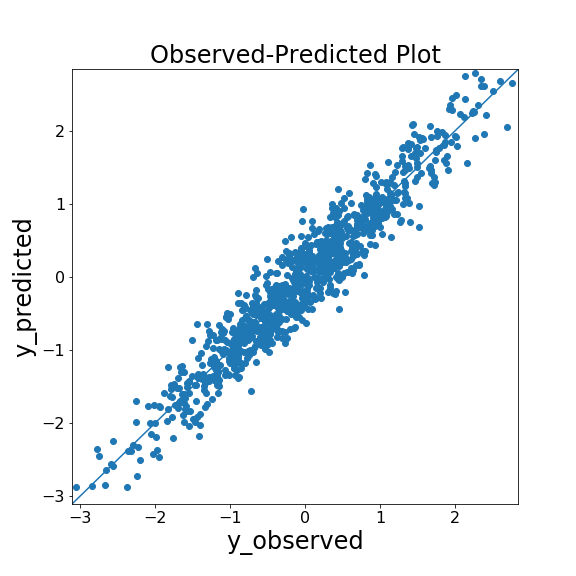
yyplot

精度評価指標に加えて回帰の様子を可視化することで、

全体の傾向(右肩下がり、両端の精度が低い等)
大きく予測を外しているデータがあるか？

等を確認できます。

精度評価指標の見方

ここまで、よく用いられる精度評価指標を紹介してきました。
この section では、それらを用いたモデルの評価の仕方について解説していきます。

RMSE と MAE の見方(数式編)

RMSE および MAE はいずれも元のデータと同じ単位を持っており、「見積もられる誤差の大きさ」を表します。
ですが、誤差の分布により、その相対的な大小に変化が生じます。

まずは、数式から両者の関係を見ていきましょう。

各実測値 \( y_{\mathrm{obs}, i} \) に対する予測値 \( y_{\mathrm{pred}, i} \) の誤差の絶対値を \( e_{i} \) とすると、RMSE² および MAE² は以下のように表せます(n はサンプル数)。

\[ e_{i} = |y_{\mathrm{obs}, i} - y_{\mathrm{pred}, i}| \] \[ RMSE^2 = \frac{\sum_{i=1}^{n} e_{i}^2 }{n} \] \[ MAE^2 = \frac{(\sum_{i=1}^{n} e_{i})^2}{n^2} \]

ここで、RMSE² と MAE² の差を考えると、
二次モーメントおよび一次モーメントを用いた分散導出の公式より[2]、
\( e_{i} \) の分散に等しいことがわかります (よって、RMSE が MAE より小さくなることはありません)。

\[ RMSE^2 - MAE^2 = \mathrm{VAR}( e_{i} ) \]

また、0 以上の値しか取らない \( e_{i} \) の平均 \(\mathrm{MEAN}( e_{i} )\) が MAE に等しいことも利用すると、 MAE に対する RMSE の比は以下のように表せます。

\[ \frac{RMSE}{MAE} = \sqrt{ 1 + \frac{\mathrm{VAR}( e_{i} )}{\mathrm{MEAN}( e_{i} )^2} } \]

では、この比はどのような値になるのが望ましいのでしょうか。

1つの例として、誤差が平均 0, 標準偏差 \( \sigma \) の正規分布に従う場合、誤差の絶対値 (\( =e_{i} \)) の分布は正規分布の絶対値の分布となります(pdf は確率密度関数)。

\[ \begin{eqnarray} \mathrm{pdf}(e) = \begin{cases} 2 \times \frac{1}{\sqrt{2 \pi} \sigma}\exp (-\frac{e^2}{2 \sigma ^2}) & (e \geqq 0) \\\ 0 & (e \lt 0) \end{cases} \end{eqnarray} \]

したがって、\( \mathrm{MEAN}( e_{i} ) \) および \( \mathrm{VAR}( e_{i} ) \) は以下のように計算できます(詳しい計算は省略)。

\[ \begin{eqnarray} \mathrm{MEAN}( e ) = \int_{0}^{\infty} e \times \frac{2}{\sqrt{2 \pi} \sigma}\exp (-\frac{e^2}{2 \sigma ^2}) de = \sqrt{\frac{2}{\pi}} \sigma \end{eqnarray} \] \[ \begin{eqnarray} \mathrm{VAR}( e ) = \int_{0}^{\infty} (e - \mathrm{MEAN}( e ))^2 \times \frac{2}{\sqrt{2 \pi} \sigma}\exp (-\frac{e^2}{2 \sigma ^2}) de = (1 - \frac{2}{\pi}) \sigma ^2 \end{eqnarray} \]

以上を用いると、MAE に対する RMSE の比は、

\[ \frac{RMSE}{MAE} = \sqrt{ 1 + \frac{(1 - \frac{2}{\pi}) \sigma ^2}{( \sqrt{\frac{2}{\pi}} \sigma )^2} } = \sqrt{\frac{\pi}{2}} \fallingdotseq 1.253 \]

となります(正規分布誤差に対する RMSE が標準偏差 \( \sigma \) と等しくなることを利用しても導出できます)。

良いモデルが構築できたとき、モデルはデータの大まかな特徴を表現し、正規分布に従うようなノイズのみが誤差として残ると考えられます。そのような場合、解析結果の RMSE と MAE の比は 1.253 に近くなります。

ただし、たとえ RMSE と MAE の比が 1.253 に近くても、以下のような場合は注意が必要です。

誤差の絶対値が大きい場合
誤差が正規分布に従わないデータを扱う場合
データ数が少ない場合

ちなみに、誤差が平均 0 、分散 \( 2 \phi ^ 2 \) のラプラス分布に従う場合、RMSE と MAE の比は

\[ \frac{RMSE}{MAE} = \sqrt{ 1 + \frac{ \phi ^2 }{ ( \phi )^2} } = \sqrt{2} \fallingdotseq 1.414 \]

となります。

RMSE と MAE の見方(yyplot 編)

次に、様々な yyplot から RMSE と MAE の関係性を検討してみます。

例として、同じ実測値 \( \left( y_{\mathrm{obs}, i} \right) \) に対して、MAE はだいたい同じ(期待値が同じ)だが、RMSE が異なる予測値 \( \left( y_{\mathrm{pred}, i} \right) \) のデータを作成し、yyplot を作図してみます。

import numpy as np
from matplotlib import pyplot as plt
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score

np.random.seed(0)

# yの正解値を作成
y_obs = np.random.normal(size=(10000, 1)).reshape(-1, 1)

# yの予測値を作成
# 正解値に異なる誤差を与えて4種類のデータを作成
y_pred_1 = y_obs + np.random.normal(scale=0.3, size=(10000, 1))
y_pred_2 = y_obs + np.random.laplace(scale=0.3 * (2 / np.pi) ** 0.5, size=(10000, 1))
y_pred_3 = y_obs + np.random.uniform(low = (-0.6) * (2 / np.pi) ** 0.5,
                                     high = 0.6 * (2 / np.pi) ** 0.5,
                                     size=(10000, 1))
y_pred_4 = y_obs + np.concatenate([np.ones((5000, 1)) * 0.3 * (2 / np.pi) ** 0.5,
                                   np.ones((5000, 1)) * (-0.3) * (2 / np.pi) ** 0.5])


# 4種類の予測値に対しyyplotを作図
yvalues = np.concatenate([y_obs, y_pred_1, y_pred_2, y_pred_3, y_pred_4]).flatten()
ymin, ymax, yrange = np.amin(yvalues), np.amax(yvalues), np.ptp(yvalues)
f, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(10, 10))
# y_pred_1
ax1.scatter(y_obs, y_pred_1, marker='.',
            label='RMSE : %.3f, MAE : %.3f \n RMSE/MAE = %.3f'%(
                mean_squared_error(y_obs, y_pred_1)**0.5, mean_absolute_error(y_obs, y_pred_1),
                mean_squared_error(y_obs, y_pred_1)**0.5 / mean_absolute_error(y_obs, y_pred_1)))
ax1.plot([ymin - yrange * 0.01, ymax + yrange * 0.01], [ymin - yrange * 0.01, ymax + yrange * 0.01])
ax1.legend(fontsize=12, loc='upper left')
ax1.tick_params(labelsize=10)
ax1.set_title('Normal distribution error', fontsize=15)
# y_pred_2
ax2.scatter(y_obs, y_pred_2, marker='.',
            label='RMSE : %.3f, MAE : %.3f \n RMSE/MAE = %.3f'%(
                mean_squared_error(y_obs, y_pred_2)**0.5, mean_absolute_error(y_obs, y_pred_2),
                mean_squared_error(y_obs, y_pred_2)**0.5 / mean_absolute_error(y_obs, y_pred_2)))
ax2.plot([ymin - yrange * 0.01, ymax + yrange * 0.01], [ymin - yrange * 0.01, ymax + yrange * 0.01])
ax2.legend(fontsize=12, loc='upper left')
ax2.tick_params(labelsize=10)
ax2.set_title('Laplace distribution error', fontsize=15)
# y_pred_3
ax3.scatter(y_obs, y_pred_3, marker='.',
            label='RMSE : %.3f, MAE : %.3f \n RMSE/MAE = %.3f'%(
                mean_squared_error(y_obs, y_pred_3)**0.5, mean_absolute_error(y_obs, y_pred_3),
                mean_squared_error(y_obs, y_pred_3)**0.5 / mean_absolute_error(y_obs, y_pred_3)))
ax3.plot([ymin - yrange * 0.01, ymax + yrange * 0.01], [ymin - yrange * 0.01, ymax + yrange * 0.01])
ax3.legend(fontsize=12, loc='upper left')
ax3.tick_params(labelsize=10)
ax3.set_title('Uniform distribution error', fontsize=15)
# y_pred_4
ax4.scatter(y_obs, y_pred_4, marker='.',
            label='RMSE : %.3f, MAE : %.3f \n RMSE/MAE = %.3f'%(
                mean_squared_error(y_obs, y_pred_4)**0.5, mean_absolute_error(y_obs, y_pred_4),
                mean_squared_error(y_obs, y_pred_4)**0.5 / mean_absolute_error(y_obs, y_pred_4)))
ax4.plot([ymin - yrange * 0.01, ymax + yrange * 0.01], [ymin - yrange * 0.01, ymax + yrange * 0.01])
ax4.legend(fontsize=12, loc='upper left')
ax4.tick_params(labelsize=10)
ax4.set_title('Level error', fontsize=15)

plt.xlim(ymin - yrange * 0.01, ymax + yrange * 0.01)
plt.ylim(ymin - yrange * 0.01, ymax + yrange * 0.01)
plt.show()

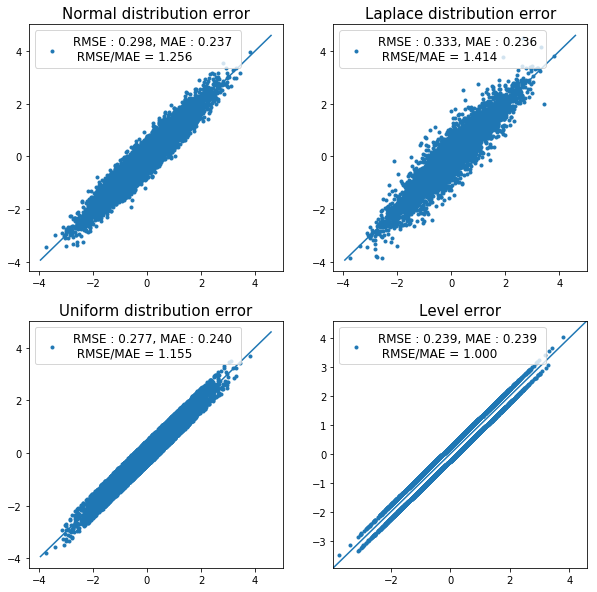
rmse-mae-comparison

上図を見ると、RMSE や MAE の挙動がよくわかります。誤差が正規分布に従う時(左上)、MAE に対する RMSE の比は \( \sqrt{\frac{\pi}{2}} \) に近くなります。
大きく予測を外すデータが多くなると(右上、ラプラス分布誤差)、RMSE が相対的に大きくなり、逆に、平均的な誤差の時(左下、一様分布誤差)、RMSE が相対的に小さくなります。すべてのデータに対する予測誤差の絶対値が等しい時(右下)、RMSE は MAE と同じ値となります。

RMSE と MAE の見方(まとめ)

数式および yyplot を用いた考察をまとめると、MAE に対する RMSE の比の見方は以下の図で要約できます。

RMSE / MAE	評価	対策 (例)
< 1.253	各サンプルについて同じような大きさの誤差が生じている可能性がある。 (SVR等で起こりやすい)	予測にバイアスを加えてみる。ハイパーパラメータを変更してみる。
= 1.253	誤差が正規分布に従う場合、適切なモデル構築ができている可能性が高い。＊誤差の絶対値も必ずチェックすること！
> 1.253	予測を大きく外しているデータが存在する可能性がある。 =1.414ならラプラス分布誤差の可能性あり。	外れ値だと思われるデータを消去する。ハイパーパラメータを変更してみる。

まとめ：良い回帰分析とは？

精度評価指標の内容及び活用方法について解説してきました。
最後に、すべての内容を踏まえて、回帰分析の良し悪しを判断する方法について 1つの案をお示しします。

精度評価指標を用いたモデルの評価

これまでの議論を元にした結論です。
精度評価指標を元にした、モデルの(相対的な)評価は、以下のような基準で行うと良いでしょう。

RMSE および MAE は小さいほど良い
R² は 1 に近いほど良いが、データセットが同じであれば RMSE に対して R² は単調減少なため同時に比較する必要はない
モデルがデータの特徴を十分に表現している場合、MAE に対する RMSE の比 \( \frac{RMSE}{MAE} \) は \( \sqrt{\frac{\pi}{2}} \) に近くなる
yyplot で予測値の分布や外れ値の有無を目視することで、指標には現れない予測の傾向をチェックできる

もちろん、モデルの評価方法はこの限りではありません(目的や対象に応じて大きく変化します)が、回帰分析を行う際にはぜひ参考にしてみてください。

[補足]その他の精度評価指標

回帰分析の精度評価指標は、紹介した以外にも多数存在しています。
多くの場合 R² 、RMSE および MAE を使用すれば事足りますが、 scikit-learn に実装されているその他の指標についても紹介しておきます。

Median Absolute Error

Median Absolute Error (あるいは Median Absolute Deviation) は以下の式で計算されます。似た意味を持つ指標である Mean Absolute Error (MAE) と略称が重なり非常に分かり辛いです。

\[ Median Absolute Error = \mathrm{Median} ( | \boldsymbol{y_{\mathrm{obs}}} - \boldsymbol{y_{\mathrm{pred}}} | ) \]

MAE と比べ、平均値ではなく中央値で scaling することで、外れ値に強く(ロバストに)なります。 scikit-learn を用いた計算は以下のようになります。

from skelearn.metrics import median_absolute_error

med_a_e = median_absolute_error(y_obs, y_pred)

Explained Variance Score

Explained Variance Score は以下の式で計算され、R² 同様、1 に近いほど精度が高いことを表します。ここで、\( \overline{(\boldsymbol{y_{\mathrm{obs}}} - \boldsymbol{y_{\mathrm{pred}}})} \) は偏差 \( (\boldsymbol{y_{\mathrm{obs}}} - \boldsymbol{y_{\mathrm{pred}}}) \) の平均値を表します。

\[ Explained Variance Score = 1 - \frac{ \mathrm{Var} (\boldsymbol{y_{\mathrm{obs}}} - \boldsymbol{y_{\mathrm{pred}}})}{ \mathrm{Var} (\boldsymbol{y_{\mathrm{obs}}})} = 1 - \frac{ \sum ((\boldsymbol{y_{\mathrm{obs}}} - \boldsymbol{y_{\mathrm{pred}}}) - \overline{(\boldsymbol{y_{\mathrm{obs}}} - \boldsymbol{y_{\mathrm{pred}}})})^2 }{ \mathrm{Var} (\boldsymbol{y_{\mathrm{obs}}}) } \]

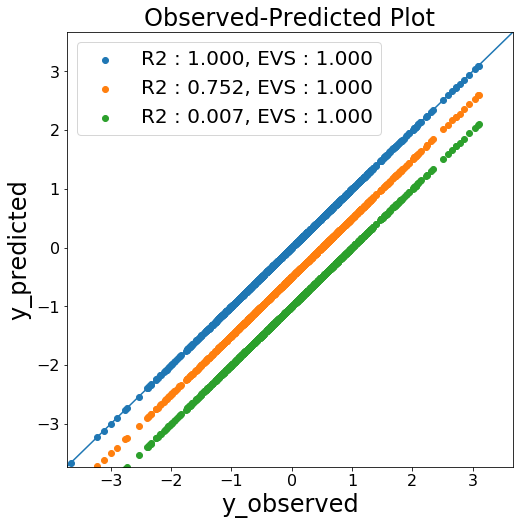
R² と大きく異なる点として、偏差の分散が小さいほど値が良好になります。
例えばすべてのデータを同じ値だけ小さく予測していた場合、Explained Variance Score は 1 となります(下図)。
線形回帰モデル \( y = ax + b \) において、傾き \( a \) が妥当かを判断する時等で使えるかもしれません。

r2-evs-comparison

scikit-learn を用いた計算は以下のようになります。

from skelearn.metrics import explained_variance_score

evs = explained_variance_score(y_obs, y_pred)

参考文献

[1]

sklearn.metrics

[2]

分散の意味と二通りの計算方法

(文責: @iwmaeda, @tawatanabe)

Instruction of chemoinformatics

ケモインフォマティクスのオンライン入門書。

精度評価指標と回帰モデルの評価

目次

数値を見る前に

回帰分析の精度評価指標

R² (決定係数)

Root Mean Squared Error (RMSE)

Mean Absolute Error (MAE)

RMSE、 MAE と最尤推定

Observed-Predicted Plot (yyplot)

精度評価指標の見方

RMSE と MAE の見方(数式編)

RMSE と MAE の見方(yyplot 編)

RMSE と MAE の見方(まとめ)

まとめ：良い回帰分析とは？

精度評価指標を用いたモデルの評価

[補足]その他の精度評価指標

Median Absolute Error

Explained Variance Score

参考文献

Instruction of chemoinformatics

ケモインフォマティクスのオンライン入門書。

精度評価指標と回帰モデルの評価

目次

数値を見る前に

回帰分析の精度評価指標

R2 (決定係数)

Root Mean Squared Error (RMSE)

Mean Absolute Error (MAE)

RMSE、 MAE と最尤推定

Observed-Predicted Plot (yyplot)

精度評価指標の見方

RMSE と MAE の見方(数式編)

RMSE と MAE の見方(yyplot 編)

RMSE と MAE の見方(まとめ)

まとめ：良い回帰分析とは？

精度評価指標を用いたモデルの評価

[補足]その他の精度評価指標

Median Absolute Error

Explained Variance Score

参考文献

R² (決定係数)