Gaussian Process

一般に機械学習による予測では、データの多く存在する領域では予測精度が高く、データの存在しない領域では予測精度が低くなります。予測精度の高さ(予測値の信頼性)は機械学習モデルにとって重要な要素ですが、一般的な回帰分析手法(Partial Least Squares, Support Vector Regression 等)ではその予測信頼性を評価できません。この問題点に対する1つの解決策として、Gaussian Process (GP) [1] があります。

Gaussian Process (GP)は、主に回帰分析を行う機械学習手法の1つです。大きな特徴として、説明変数 \( X \) の入力に対し目的変数 \( y \) の予測値の分布を正規分布として出力します。

\[ f(X)=N(\mu, \sigma^2) \]

出力される正規分布の標準偏差 \( \sigma \) は、目的変数 \( y \) の値の”不確かさ”を表します。標準偏差 \( \sigma \) が小さいデータは不確かさが小さい(予測信頼性が高い)、大きいデータは不確かさが大きい(予測信頼性が低い)と判断でき、予測値 + 予測値の信頼性 を考慮した回帰分析を行うことができます。

GP は、実験計画法の分野で ベイズ最適化 [2] として広く用いられています。本ページでは python での GP モデル構築、およびGPを用いた実験計画法について紹介します。

なお、回帰式の導出、および少し特殊な kernel 関数の構成については詳説しません。こちらについては以下の資料が詳しいです [1], [3]。

概要

以下の順番で説明していきます。GPモデルの構築には scikit-learn に実装されている GaussianProcessRegressor を用います。

  1. データセットの作成
  2. GPモデルの構築
  3. GPモデルを用いた予測
  4. GPモデルを用いた実験計画法

データセットの作成

今回は、scikit-learn の tutorial でも使用されている [4] 以下の関数に対し GP モデルの構築を行います。モデル構築用データは、\( x=(1, 3, 5, 6, 7, 8) \) の6点です。

\[ y = x \sin(x) \]

import numpy as np
from matplotlib import pyplot as plt


# 解析関数の定義
def f(X):
    return X * np.sin(X)

# データセットの作成
X = np.atleast_2d([1., 3., 5., 6., 7., 8.]).T
y = f(X)

# データセットの可視化
plot_X = np.atleast_2d(np.linspace(0, 10, 1000)).T
fig = plt.figure(figsize=(8, 6))
plt.plot(plot_X, f(plot_X), 'k')
plt.plot(X, y, 'r.', markersize=16)
plt.xlabel('$x$', fontsize=16)
plt.ylabel('$y$', fontsize=16)
plt.ylim(-8, 12)
plt.legend(['$y = x*\sin(x)$', 'Observed values'], loc='upper left', fontsize=16)
plt.tick_params(labelsize=16)
plt.show()

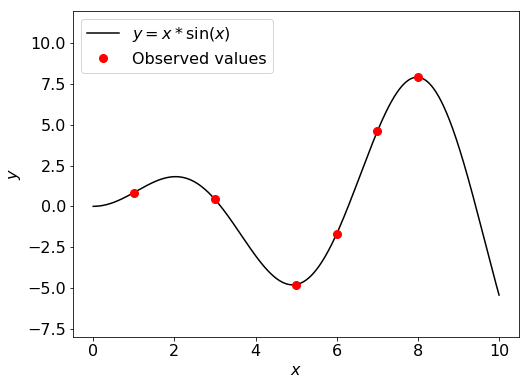
test-function

GPモデルの構築

目的変数の scaling を行った後に、GP モデルの定義および学習を行います。
今回は kernel 関数に以下の構成を用いました。

\[ \rm (Constant \ Kernel) × (RBF \ Kernel) + (White \ Kernel) \]

Constant Kernel が定数 kernel、RBF Kernel がRadius Based Function kernel (あるいは Gaussian kernel)を表します。White Kernelは目的変数のノイズの大きさに関する kernel 関数で、(今回は関係ありませんが)データセットにノイズが含まれる場合に重宝します。White Kernel を導入する場合、GaussianProcessRegressor の引数 alpha を0とすることに注意してください。

GaussianProcessRegressor の fit 関数を実行すると、GP モデルの学習が行われます。特に指定がなければ、モデル構築用データに対する尤度が最大となるように kernel 関数のパラメータが最適化されます。

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import ConstantKernel, RBF, WhiteKernel
from sklearn.preprocessing import StandardScaler

# データのscaling
# scikit-learnに実装されているStandardScalerを利用
# 説明変数のscalingはしなくても問題ありませんが、目的変数のscalingは必須です(平均の事前分布を与えるのが難しいため)
scaler_y = StandardScaler().fit(y)

# GPモデルの構築
kernel = ConstantKernel() * RBF() + WhiteKernel()
gpr = GaussianProcessRegressor(kernel=kernel, alpha=0)
gpr.fit(X, scaler_y.transform(y))

# kernel関数のパラメータの確認
print(gpr.kernel_)
# 1.36**2 * RBF(length_scale=3.07) + WhiteKernel(noise_level=0.061)

GPモデルを用いた予測

構築した GP モデルを用いて、各 \( x \) に対する \( y \) の値の95%信頼区間を予測します。
GaussianProcessRegressor の predict 関数は、return_std=True とすることで予測される目的変数の分布の平均および標準偏差を出力します。

# plot_Xに対する平均および標準偏差の予測
pred_mu, pred_sigma = gpr.predict(plot_X, return_std=True)
pred_mu = scaler_y.inverse_transform(pred_mu)
pred_sigma = pred_sigma.reshape(-1, 1) * scaler_y.scale_

# 各xに対する95%信頼区間を表示
fig = plt.figure(figsize=(8, 6))
plt.plot(plot_X, f(plot_X), 'k')
plt.plot(X, y, 'r.', markersize=16)
plt.plot(plot_X, pred_mu, 'b')
# データが正規分布に従う場合、95%信頼区間は平均から標準偏差の1.96倍以内の区間となる
plt.fill_between(plot_X.squeeze(), (pred_mu - 1.9600 * pred_sigma).squeeze(), (pred_mu + 1.9600 * pred_sigma).squeeze())
plt.xlabel('$x$', fontsize=16)
plt.ylabel('$y$', fontsize=16)
plt.ylim(-8, 12)
plt.legend(['$y = x*\sin(x)$', 'Observed values', 'Predicted mean', '95% confidence interval'], loc='upper left', fontsize=16)
plt.tick_params(labelsize=16)
plt.show()

出力されたグラフを見れば分かる通り、モデル構築用データが存在する領域では95%信頼区間が狭く(予測された標準偏差が小さく)、モデル構築用データが存在しない領域では95%信頼区間が広く(予測された標準偏差が大きく)なっています。

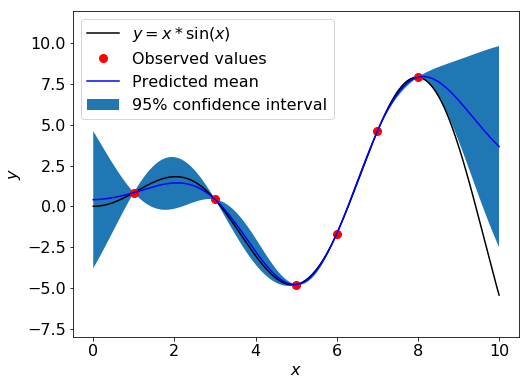
confidence-interval

GPモデルを用いた実験計画法

GP を用いて、簡単な実験計画法(Experimental Design)を行ってみましょう。

GPを用いた実験計画法は一般的にベイズ最適化と呼ばれ、少ない実験回数での設計変数最適化 [5] や機械学習モデルのハイパーパラメータ最適化 [6] に活用されています。
ベイズ最適化では、GP モデルで予測された目的変数 \( y \) の分布を元に、Acquisition Function と呼ばれる指標を計算し、Acquisition Function が最大となる点を次の実験対象として選択します [2]。 目的変数の最小化を目指す場合、予測された \( y \) の分布の平均が小さく(予測値が小さい)、標準偏差が大きい(不確かさが大きい)ほど Acquisition Function は大きな値を取ります。

構築した GP モデルを用いて、より小さい観測値が得られる説明変数 \( x \) の値を探索します。今回は Acquisition Function として、Expected Improvement (EI) を用います。EI は以下の式で計算され、モデル構築用データの最小値を下回る量の期待値を表します。ここで、 \( \xi \) は定数(モデル構築用データの標準偏差の1%ほどが推奨)、\( \Phi \) 、 \( \phi \) はそれぞれ、標準正規分布の累積分布関数 (CDF) および 確率密度関数 (PDF) を表しています。

\[ Z = \frac{y_{min}-\mu-\xi}{\sigma} \] \[
EI = \sigma Z \Phi (Z) + \sigma \phi (Z) \]

先程構築したGPモデルを用いて、各 \( x \) に対して、EIを計算します。

from scipy.stats import norm

# 各xに対して、Expected Improvement(EI)を計算

# モデル構築用データの最小値および標準偏差
min_y = np.min(y)
std_y = np.std(y)

# xiの値を決定
xi = std_y * 0.01

# EIを計算
# 単に EI = pred_sigma * Z * np.array([norm.cdf(z) for z in Z]) +
#          pred_sigma * np.array([norm.pdf(z) for z in Z])
# としていないのは、予測された標準偏差が0の場合EIの計算ができないため
EI = np.zeros(len(pred_mu))
ind = np.where(pred_sigma != 0)[0]
pred_mu = pred_mu[ind]
pred_sigma = pred_sigma[ind]
Z = (min_y - pred_mu - xi) / pred_sigma
EI.flat[ind] = pred_sigma * Z * np.array([norm.cdf(z) for z in Z]) + pred_sigma * np.array([norm.pdf(z) for z in Z])

# EIをプロット
fig = plt.figure(figsize=(8, 6))
plt.plot(plot_X, EI)
plt.xlabel('$x$', fontsize=16)
plt.ylabel('Expected Improvement', fontsize=16)
plt.tick_params(labelsize=16)
plt.show()

# x=[4, 6]の区間でEIの一番高いx
best_x = plot_X[400:600][np.argmax(acq[400:600])]
print(best_x)
# 4.83483483

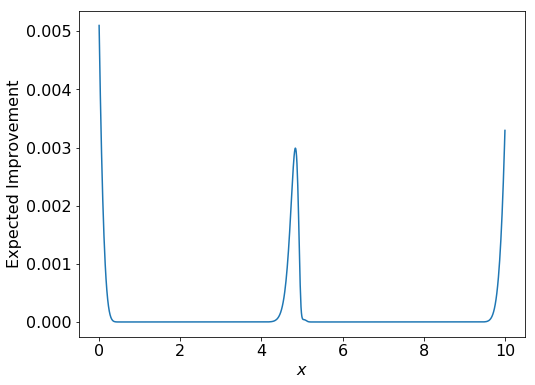
expected-improvement

探索区間の両端及び中央部で EI の値が高く(探索対象としてふさわしく)計算されています。\( x=0 \) 付近はやや過剰に評価されているものの \( f(x) \) が減少している区間、残りの2つの区間は実際に \( f(x) \) が小さい値をとっていることから、良い探索ができているといえます。
また、中央部で EI が最小となる \( x \) は約4.835。\( f(x) \) が実際に極小値をとる \( x \fallingdotseq 4.913 \) に近い値を示しています。

まとめ

今回は簡単な関数に対し GP を用いたモデル構築および実験計画法を行いました。同様の手法はより複雑な関数や実データに対しても適用できます。ぜひ活用してみてください。

GP関連パッケージ

参考文献

[1]

C. E. Rasmussen, C. K. I. Williams, G. Processes, M. I. T. Press, M. I. Jordan, Gaussian Processes for Machine Learning, 2006.

[2]

ベイズ最適化入門

[3]

ガウス過程による回帰(Gaussian Process Regression, GPR)～予測値だけでなく予測値のばらつきも計算できる！～

[4]

Gaussian Processes regression: basic introductory example

[5]

A. Nakao, H. Kaneko, K. Funatsu, Development of an Adaptive Experimental Design Method Based on Probability of Achieving a Target Range through Parallel Experiments, Industrial & Engineering Chemistry Research, 55(19), 5726-5735.

[6]

Bayesian Optimization for Hyperparameter Tuning

(文責: @iwmaeda)