最尤推定
本項では最尤推定による推定モデル構築について、機械学習でよく用いられるモデル構築手法との関連を中心に解説します。 (尤度の概念を用いるため、事前に尤度の項に目を通しておくことをお勧めします)
本項で取り扱う手法は最尤推定、最小二乗法、Bayes推定です。Bayes推定はBayesの定理に基づき、データとして表せない情報(経験から得られる知見等)も活用できる手法として、近年注目を集めています。
実は最小二乗法は最尤推定の特別な場合に相当し、最尤推定はBayes推定の特殊な場合に当たります。
本項では、このような手法同士の関係や各手法において置かれる仮定について解説します。
概要と見出し
本項では、以下の順番で説明していきます。
例-線形単回帰モデル
尤度の項と同様に、変数\(y\)を変数\(x\)から推定する回帰モデル\(f\)を構築することを考えます。\(f\)はパラメタ\(m\)を持つとし、モデルの誤差\(e = y - \hat{y}\)は確率分布\( p_{e}(e)\)に従うとします。
いま、 \((x, y)\)の観測値\(\boldsymbol{d} = [(x_{1}, y_{1}); …; (x_{N}, y_{N})]\)が得られたとき、パラメタ\(m\)の尤度\(L\)は以下のように表されます。 \[ L(m|\boldsymbol{d})=\prod_{i=1}^N p_{e} (y_{i}-f(x_{i},m)) \] この尤度を最大化することで妥当なモデルを得られることを尤度の項で示しました。実際に尤度を最大化する\(m\)が満たすべき条件を求めてみましょう。
ただ、そのためには誤差の確率分布\(p_{e}(e)\)を定めなければなりません。ここでは、例として \(p_{e}(e)\)を平均0の正規分布 とします。
正規分布の確率密度関数は以下の式で与えられます。 \[ p(x)=\left(\frac{1}{2\pi \sigma^{2}}\right)^{\frac{1}{2}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right) \]
ここで、\(\mu\), \(\sigma^{2}\)は正規分布の平均及び分散です。\(\mu=0\)として、この式を尤度の式に代入します。
\[ \begin{eqnarray} L(m|\boldsymbol{d})&=&\prod_{i=1}^N\left(\frac{1}{2\pi \sigma^{2}}\right)^{\frac{1}{2}} \exp\left(-\frac{||y_i-f(x_i,m)||^2}{2\sigma^2}\right) \\ &=&\left(\frac{1}{2\pi \sigma^{2}}\right)^{\frac{N}{2}} \exp\left(-\frac{1}{2\sigma^2}\sum_{i=1}^N ||y_i-f(x_i,m)||^2\right) \end{eqnarray} \]
ここで、尤度の対数を考えます。ある関数の対数の最大化はその関数の最大化と同値なので、対数に置き換えても議論に影響はありません。 \[ \logL(m|\boldsymbol{d})=\frac{N}{2}\log\left(\frac{1}{2\pi \sigma^{2}}\right)-\frac{1}{2\sigma^2}\sum_{i=1}^N ||y_i-f(x_i,m)||^2 \] 上の式より、尤度を\(m\)について最大化するには\(\sum_{i=1}^N ||y_i-f(x_i,m)||^2\) を最小化すればよいことが分かります。つまり二乗誤差を最小化すればよいことになります。これは最小二乗法に他なりません。
つまり、最小二乗法 = 誤差に平均0の正規分布を仮定した場合の最尤推定 です。二乗誤差を最小化するようにモデルを構築することは統計学や機械学習ではよくありますが、それは モデリングできない部分はバイアスのない正規分布に従うと仮定している ことになります。
そのため、誤差が正規分布に従わない、あるいはモデリングできないバイアスがあるようなデータに対して最小二乗法でモデルを構築することは、必ずしも適切ではないといえます。生態などの分野のデータでは誤差が正規分布に従わないことも多い[1]ため、注意しましょう。予測値と実測値の誤差のプロットが明らかに正規分布から外れている場合は、最小二乗法が適切でないことを考慮した方がよいかもしれません。
また誤差が正規分布以外の分布に従うと分かった場合は、上式における\(p(x)\)をその分布の確率密度関数に置き換えて尤度を求め、それを\(m\)について最大化することで同様に最尤推定値を求められます。ただし、最小二乗法のようにシンプルな形で\(m\)の条件式が求まるとは限りません。
応用例-モデルの妥当性評価
また、上記の対数尤度の表式を分散\(\sigma^{2}\)で微分することで、\(\sigma^{2}\)についても最尤推定値を求めることができます。
\[ \frac{\partial \log{L(m|\boldsymbol{d})}}{\partial \sigma^{2}}=-\frac{N}{2\sigma^{2}}+\frac{\sum_{i=1}^N ||y_i-f(x_i,m)||^2}{2(\sigma^{2})^{2}} \]
この微分値を0とする\(\sigma^{2}\)は以下の式で与えられます。
\[ \sigma^{2}=\frac{\sum_{i=1}^N ||y_i-f(x_i,m)||^2}{N} \]
この\(\sigma^{2}\)の推定値は、予測誤差の分布の分散の推定値です。一方、計測機器の測定誤差や実験誤差などから、予測誤差の分布をある程度推定できる場合があります。
そこで、モデルを構築した後に\(\sigma^{2}\)を推定し、想定される予測誤差の程度と比較することでモデルの妥当性を評価できます。以下に例を示します。
import numpy as np
from numpy import random as rd
# Make data
rd.seed(7)
n_data=50
x = rd.rand(n_data,1)
x = x*4-2 # xの範囲を-2~2に
y = 3*x**2-2 # y = 3x^2-2
y += rd.randn(n_data,1) # yに平均0, 標準偏差1の正規乱数を加算
yはxの2次関数であり、分散1の正規乱数がノイズとして加えられています。このデータに1次式、2次式、30次式のモデルを当てはめてみます。
from matplotlib import pyplot as plt
from sklearn import linear_model
# Make input variable of model
def polynominal(x,n):
# 変数x及びそのべき乗(n乗まで)を並べたndarrayを返す関数
n_data = np.shape(x)[0]
p = np.tile(np.arange(1,n+1),(n_data,1)) # 指数を表すndarray
x_poly = np.tile(x,(1,n))**p
return x_poly
x_2 = polynominal(x,2)
x_30 = polynominal(x,30)
# Construct model
model_1 = linear_model.LinearRegression()
model_1 = model_1.fit(x,y)
model_2 = linear_model.LinearRegression()
model_2 = model_2.fit(x_2,y)
model_30 = linear_model.LinearRegression()
model_30 = model_30.fit(x_30,y)
# Compute predicted y
x_grid = np.linspace(min(x),max(x),1001).reshape((1001,1)) # データの存在範囲を1000等分した点を取る。
x_grid_2 = polynominal(x_grid,2)
x_grid_30 = polynominal(x_grid,30)
ypred_grid = model_1.predict(x_grid)
ypred_grid_2 = model_2.predict(x_grid_2)
ypred_grid_30 = model_30.predict(x_grid_30)
ypred = model_1.predict(x)
ypred_2 = model_2.predict(x_2)
ypred_30 = model_30.predict(x_30)
# plot
fig = plt.figure(figsize=(8, 8))
plt.plot(x_grid,ypred_grid,color='g',linewidth=1)
plt.plot(x_grid,ypred_grid_2,color='r',linewidth=1)
plt.plot(x_grid,ypred_grid_30,color='b',linewidth=1)
plt.scatter(x,y,marker = '.',color='k',s=50)
plt.xlabel('$x$', fontsize=16)
plt.ylabel('$y$', fontsize=16)
plt.tick_params(labelsize=14)
plt.ylim(-5, 12)
plt.legend(['predict(degree=1)','predict(degree=2)','predict(degree=30)','Observed data'], loc='best', fontsize=12)
# 分散推定値の計算
sigma_estimated=sum(((np.tile(y,(1,3))-np.c_[ypred,ypred_2,ypred_30])**2))/n_data
plt.text(0,6,'$\sigma$={0:5.3f}'.format(sigma_estimated[0]),ha = 'center',va = 'top', fontsize = 16,color = 'g')
plt.text(0,4.5,'$\sigma$={0:5.3f}'.format(sigma_estimated[1]),ha = 'center',va = 'top', fontsize = 16,color = 'r')
plt.text(0,3,'$\sigma$={0:5.3f}'.format(sigma_estimated[2]),ha = 'center',va = 'top', fontsize = 16,color ='b')
plt.show()
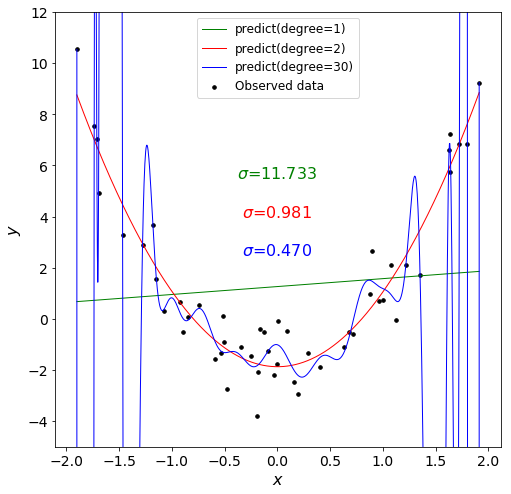
1次式のモデルでは、分散の予測値は本来の10倍以上という非常に大きな値となっています。もしデータに含まれるノイズの分散(ばらつき)がある程度推定できるのなら、このモデルは明らかに不適切であると判断できます。
一方、30次式のモデルは分散の予測値が本来の半分以下となっています。これはモデルがノイズ部分にまで適合していることを示しています。
一方、2次式モデルでは分散の値が1に近くなっており、予想されるノイズの大きさと合致しています。
このように、分散の予測値を想定される分散と比較することでモデルの妥当性を判断することができます。サンプルのノイズの様子に大きく依存するため厳密な評価は難しいですが、上記の例の1次式のように、明らかに予想される値とかけ離れている場合はモデルの説明変数などを見直すことをお勧めします。
Bayes推定との関係性
近年、推定の分野では最尤推定に代わりBayes推定がよく用いられています。本項では、最尤推定とBayes推定の関連性を簡単に説明します。関連する事柄を扱った文献は複数[2][3]あるため、詳しく学習したい方はそちらも参照ください。
これまでの議論と同様に、データ\(d\)を用いて推定モデルのパラメタ\(m\)を最適化することを考えます。最尤推定では尤度を最大化しますが、Bayes推定では事後確率という値を最大化します。事後確率とは、 ある観測値の下である仮説が正しい確率 と定義されます。上記の例では、データ\(d\)が得られた場合にモデルのパラメタ\(m\)が正しい確率となります。 Bayes推定では、以下に示すBayesの定理を用いて事後確率\(p(m|\boldsymbol{d})\)を計算します。
\[ p(m|\boldsymbol{d})=\frac{p(\boldsymbol{d}|m)p(m)}{p(\boldsymbol{d})} \]
ここで、\(p(\boldsymbol{d}|m)\)はパラメタ\(m\)の下でデータ\(\boldsymbol{d}\)が得られる条件付確率であり、尤度と全く同一の値です。(こちらを参照)
\(p(m)\)はパラメタが\(m\)である確率、\(p(\boldsymbol{d})\)はデータが\(\boldsymbol{d}\)となる確率であり、これらは事前確率と呼ばれます。事前確率はデータや過去の経験などから決定されます。
(例:パラメタ\(m\)は大きな値を取らない(方が望ましい)ため、平均0の正規分布とする)
ただし\(p(\boldsymbol{d})\)は\(m\)とは無関係な値であるため、事後確率を最大化するには結局 尤度と\(m\)の事前確率の積 を最大化する\(m\)を探索すればよいことが分かります。
ここで、\(m\)の事前分布\(p(m)\)が\(m\)に依存しない(\(m\)が一様に分布している)場合を考えます。すると、\(m\)を変化させても事前確率は一定であるため、尤度を最大化することで事後確率も最大化できます。
つまり、最尤推定とは 事前分布が一様であるBayes推定 といえます。Bayes推定では経験やデータから\(m\)に関して何らかの知見がある場合、一様ではない\(p(m)\)を定義することでその知見を予測に反映することができます。
一方最尤推定は\(m\)について全く仮定を置かず、手持ちのデータのみから尤もらしい\(m\)を推定します。したがってデータが十分にあるならば、最尤推定を用いることで事前分布なるものを推定せずとも適切なパラメタを決定できます。しかし多くの場合データが十分に存在しないため、データ以外の知見も活用できるBayes推定が用いられることが増えてきました。
まとめ
本項では最尤推定法の概念について説明し、モデル構築においてしばしば用いられる最小二乗法との関連を解説しました。また、Bayes推定との関連についても簡単に記述しました。 一般に用いられる最小二乗法は、「背景にある事象を手持ちのデータが完全に表現しており、モデリングできない部分は正規分布に従う誤差とする」という仮定を置いていることになります。このように普段何気なく用いる手法は、実はそれなりの仮定を置いていることが往々にしてあります。手法を使う前に、対象とするデータがその仮定を満たしているか確認することが非常に重要といえます。 本項で示したように、最尤推定は統計学や機械学習の基礎となる概念です。その考え方を知ることで手法の背景や仮定の理解につながるので、ぜひ理解して適切な解析の参考にしてください。
参考文献
(文責: @tawatanabe)