Random Forest
この記事では、機械学習における非線形分類・回帰手法の一つ、Random Forest[1]を紹介します。
Random Forestの特徴
Random Forestのしくみ
‐決定木
‐アンサンブル学習
Random Forestの実践
1.分類
2.回帰
3.その他の機能
まとめ
Random Forestの特徴
さまざまな機械学習手法の中で、Random Forestの利点は
・調整すべきパラメータがほとんどない
・変数選択の必要がない
といった点です。
分類と回帰のどちらにも使えます。
弱点としては、データ数が少ない場合に過学習になりやすい傾向があります。
Random Forestのしくみ
Random Forestは、複数のモデルを組み合わせてより強力なモデルを作る アンサンブル学習 手法の一つです。 組み合わせる元のモデルとしては 決定木 を用います。
決定木
決定木とは、条件に基づいてデータを分割していく学習方法です。 「ある変数について、ある閾値で予測結果が枝分かれする」ということを繰り返して予測モデルを構築します。 決定木による分類のイメージを示します。下図は特徴量が\( X1 \)、\( X2 \)の2個であるデータを、2種類のグループに分類しています。分割後の各領域の純度が最も高くなる(偏りが最も大きくなる)変数・閾値で枝分かれを作っていき、決定木を構築します。

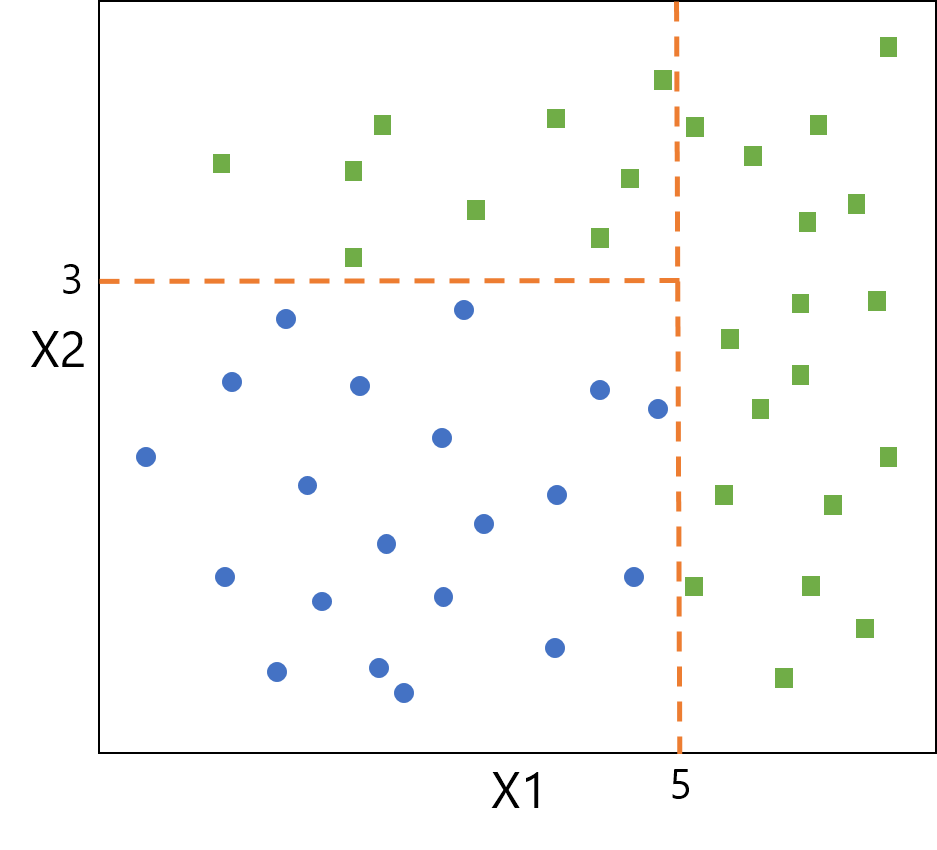
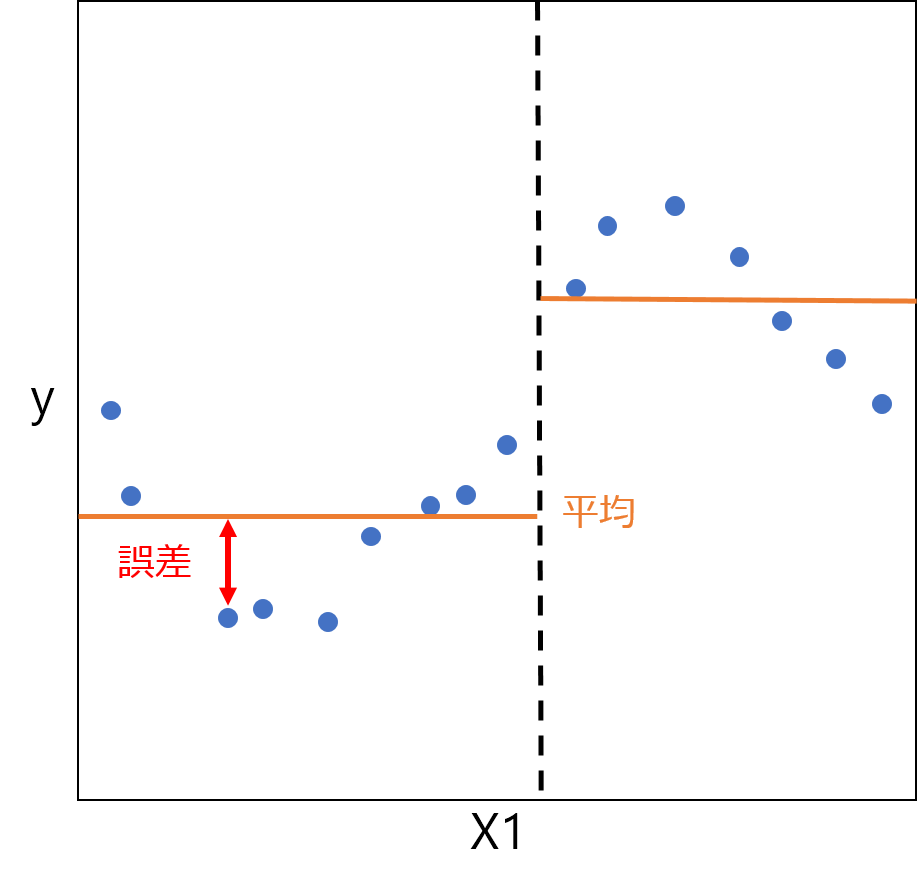
回帰のイメージを下図に示します。この例では特徴量は\( X1 \)の1個のみで、縦軸は目的変数\( y \)を表します。青い点が実データに対応します。 回帰の場合は、左図に示すように、各データと平均との誤差の二乗和が最小となる変数・閾値で分けます。これを繰り返して最終的には、右図の橙色の線のような回帰モデルが作られます。
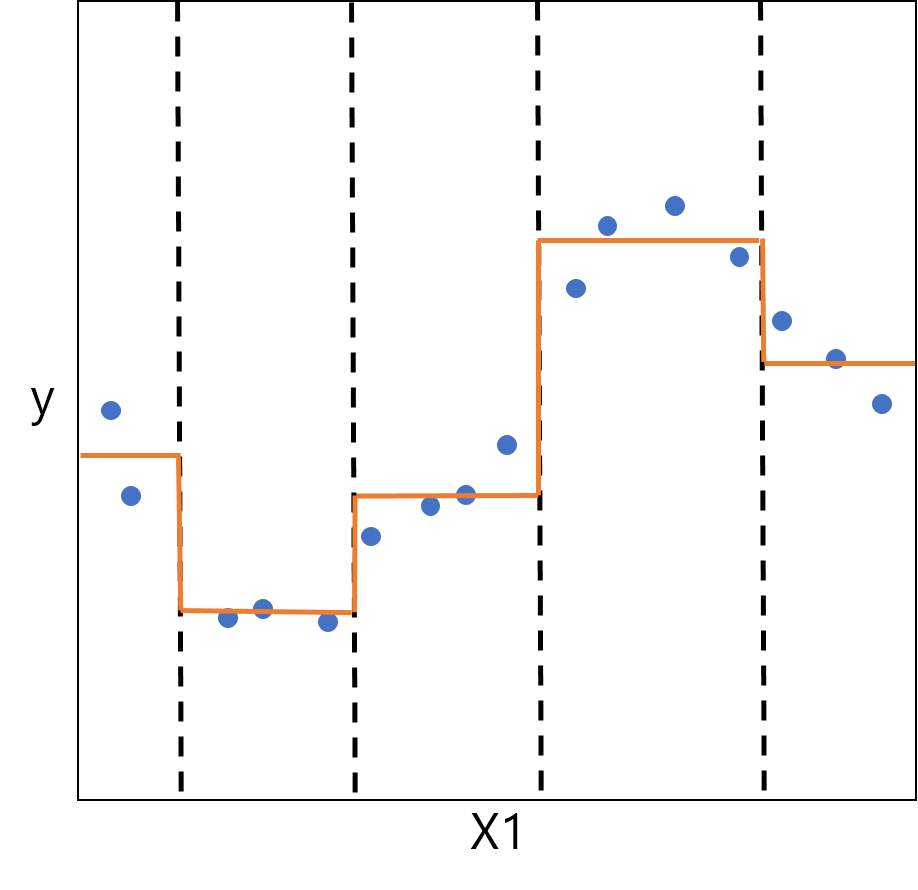
このように決定木は、データの分類にも、値の予測にも用いられます。 決定木はモデル構築の際に変数選択がなされているので、事前の変数選択が必要ないという利点があります。
アンサンブル学習
アンサンブル学習とは、複数のモデルを組み合わせてより強力なモデルを作る手法です。 前項で説明した決定木によるモデルは分類境界や回帰曲線がカクカクしていますが、これを複数組み合わせて平均をとることで比較的滑らかなモデルを作ることができます。 Random Forestでは、 ブートストラップサンプリング という方法でデータを選択しています。これは、一つのサンプル集合から重複を許してサンプリングし、新たなサンプル集合とする方法です。\( m \)個のデータから重複を許して\( m \)個とって学習データとします。 重複を許すので結果的に選ばれないデータも存在し、これを OOB(Out Of Bag) といいます。 このようなサンプリングを繰り返し行ってできる多数の学習データセットについて、それぞれ決定木を構築します。それらの予測結果の平均が最終的な予測結果となります。
Random Forestの実践
機械学習ライブラリscikit-learnを用いて、実際にRandom Forestを用いた解析を行います。
1. 分類:RandomForestClassifier
まずはデータセットを用意します。 scikit-learnのiris(アヤメ)データセットを使用します。次のように記述することで、変数「iris」にデータセットの情報が格納されます。
from sklearn import datasets
iris = datasets.load_iris()
feature_name(特徴名)と、target_name(分類名)を見てみます。
print(iris['feature_names'])
print(iris['target_names'])
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
['setosa' 'versicolor' 'virginica']
各アヤメのデータとして「ガクの長さ・幅、花弁の長さ・幅」の4つの特徴量が記されており、 そのアヤメの品種が3種類の分類のうちどれであるかがラベル付けされています。 dataには、150のアヤメそれぞれの特徴量の値が登録されています。 targetには、各アヤメの品種ラベルが「0, 1, 2」の番号で登録されています。
print(iris['data'])
print(iris['target'])
それでは、「データの特徴量の値を元に、アヤメを3種類に分類する」モデルを構築します。
# X,yをそれぞれランダムに、学習データとテストデータに分ける(学習:テスト = 0.8:0.2)
from sklearn.model_selection import train_test_split
X = iris['data']
y = iris['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8)
# 学習データを使ってモデルを構築する
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier()
clf.fit(X_train, y_train)
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=None, max_features='auto', max_leaf_nodes=None,
min_impurity_split=1e-07, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
n_estimators=10, n_jobs=1, oob_score=False, random_state=None,
verbose=0, warm_start=False)
・max_depth:木の深さ。どこまで枝分かれさせるか。 ・n_estimators:木の数。 などのパラメータを設定できます。精度や計算時間を考慮し、必要に応じて変更します。 各パラメータについて、詳しくは公式ドキュメントを参照してください。 それでは、このモデルに沿ってテストデータの分類を行い、精度を確認します。
# テストデータのyの予測値を求める
y_predicted = clf.predict(X_test)
# 実際のyの値と予測値を比較して、正答率を確認する
from sklearn import metrics
accuracy = metrics.accuracy_score(y_test, y_predicted)
print(accuracy)
0.933333333333
2. 回帰:RandomForestRegressor
scikit-learnのboston(ボストン市の住宅価格)データセットを使用します。
from sklearn import datasets
boston = datasets.load_boston()
feature_name(特徴名)を見てみます。
print(boston['feature_names'])
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
各データには、各物件の人口統計に関する13の特徴量が記されています。 dataには、各物件の特徴量の値が登録されています。 targetには、各物件の価格が登録されています。 それでは、「データの特徴量の値を元に、住宅の価格を予測する」モデルを構築します。
# X,yを、それぞれランダムに学習データとテストデータに分ける(学習:テスト = 0.8:0.2)
from sklearn.model_selection import train_test_split
X = boston['data']
y = boston['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8)
# 学習データを使ってモデルを構築する
from sklearn.ensemble import RandomForestRegressor
regr = RandomForestRegressor()
regr.fit(X_train, y_train)
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_split=1e-07, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
n_estimators=10, n_jobs=1, oob_score=False, random_state=None,
verbose=0, warm_start=False)
各パラメータについて詳しくは、分類と同様に公式ドキュメントを参照してください。 それでは、このモデルに沿ってテストデータのy値を予測し、精度を確認します。
# テストデータのyの予測値を求める
y_predicted = regr.predict(X_test)
# 実際のyの値と予測値を比較して、テストデータに関するR2決定係数を確認する
from sklearn import metrics
R2test = metrics.r2_score(y_test, y_predicted)
print(R2test)
0.886998700932
3. その他の機能
以下に挙げるのは、Random Forestの機能の一部です。 分類でも回帰でも用いることができますが、ここではボストン市住宅価格予測の回帰モデルを例に挙げて紹介します。
・oob_score
Random forestの各決定木を作る際に、モデル構築に用いられなかったサンプルを OOB(Out Of Bag)と言います。 この OOB をバリデーション用データのように用いて、バリデーションスコアを求めることができます。
from sklearn import datasets
boston = datasets.load_boston()
# X,yを、それぞれランダムに学習データとテストデータに分ける(学習:テスト = 0.8:0.2)
from sklearn.model_selection import train_test_split
X = boston['data']
y = boston['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.8)
# 学習データを使ってモデルを構築する
from sklearn.ensemble import RandomForestRegressor
# oob_score=True にパラメータを変更する(デフォルト値はFalse)
regr = RandomForestRegressor(oob_score=True)
regr.fit(X_train, y_train)
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_split=1e-07, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
n_estimators=10, n_jobs=1, oob_score=True, random_state=None,
verbose=0, warm_start=False)
# oob_scoreを求める
oob_score = regr.oob_score_
print(oob_score)
0.733683861457
・feature_importance
Random Forest では、各変数の重要度(feature_importance)を求めることができます。 以下のようにして、13種類の特徴量がモデル構築にそれぞれどれだけ寄与したかを求めることができます。
# feature_importanceを求める
feature_importances = regr.feature_importances_
print(feature_importances)
[ 0.02799019 0.00084522 0.00413129 0.00120428 0.00946862 0.60004269
0.01418742 0.05035083 0.00475161 0.01729037 0.01621295 0.01394745
0.23957708]
分かりやすいようにグラフにします。
import numpy as np
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 5))
plt.ylim([0, 1])
y = feature_importances
x = np.arange(len(y))
plt.bar(x, y, align="center")
plt.xticks(x, boston['feature_names'])
plt.show()
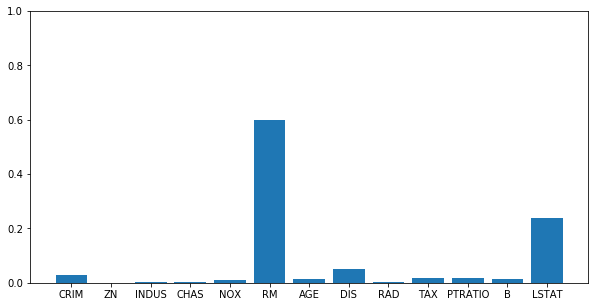
‘RM’や ‘LSTAT’という特徴量が重要であったと分かります。
※feature_importance算出のしくみ
feature_importanceの算出にもOOBが利用されています。 OOBの、ある変数\( x \)の値をシャッフルして予測を行います。 その\( x \)の値がでたらめになるのでふつう予測精度は下がります。同様のことを他の変数についても行います。 その結果シャッフル前後で大きく予測精度が変化した変数が、重要な変数であると判断されます。 逆に「シャッフルしてもたいして精度の変わらない変数は、もともとこの予測モデルにとって重要な変数ではなかった」ということになります。
まとめ
分類・回帰手法として用いられるRandom Forestのしくみを説明し、scikit-learnのRandom Forestモジュールの使い方を紹介しました。 各パラメータの設定やメソッドのすべてを紹介することはできませんので、scikit-learnの公式ドキュメントを参照しながらいろいろと試してみてください。
公式ドキュメント: ・RandomForestClassifier ・RandomForestRegressor
参考:
L. Breiman, Random forests. Machine learning, 2001, 45.1: 5-32
(文責: @fsakata)