Partial least Squares
Partial Least Squares(PLS)とは
Partial Least Squares(PLS)は線形回帰手法の一種であり、回帰分析に広く用いられています。 説明変数を互いに無相関になるように線形変換した変数(潜在変数)を用いることが特徴です。 PLSには以下のような特徴があります。
・共線性に対応できる
共線性とは、説明変数同士の相関が強い場合、回帰平面が一意に決まりにくく、回帰モデルが不安定になってしまう現象です。 PLSは説明変数を互いに無相関な変数に変換するため、共線性の問題が生じません。
・サンプル数が説明変数より少ない場合でもモデルを構築できる
データ数が説明変数の数より少ない場合、通常の線形回帰では一意に回帰式を決定できません。 PLSは潜在変数を使用しますが、その際使用する潜在変数の数を減らすことで、サンプル数が説明変数よりも少ない場合も 全ての説明変数を考慮に入れつつモデルを構築できます。
・ノイズに強い
詳細は後述しますが、PLS法の潜在変数は目的変数の回帰に貢献する変数を優先的に作成します。 そのため、潜在変数のうち重要なもののみを使用すれば、ノイズなど予測に貢献しない部分をモデルから除外できます。
回帰式
以下、説明変数をX、目的変数をyとします。また、潜在変数の数(PLSの成分数)をA、潜在変数をT、 それぞれの座標軸Xに対して射影したものをP、yに対して射影したものをqとします。 PLSの基本となるのは、以下の2式です。 \[ X = TP^{T}+E -(1) \]
\[ y = Tq + f -(2) \]
ただし、\(E\), \(f\)はそれぞれ\(X\), \(y\)の誤差項です。 また、\(T\)は次の(3)式で定義されます。
\[ T=XW-(3) \]
\[ [t_{1},t_{2},…t_{A}]=X[w_{1},w_{2},…w_{A}] \] ただし、\(||w_{i}||=1\)という制約条件が付きます。 ここでA=1とすると、(1),(2)式は(4),(5)式のようになります。
\[ X = t_{1}p_{1}^{T}+E_{1}-(4) \]
\[ y = t_{1}q_{1}+f_{1} -(5) \]
\(E_i\), \(f_i\)は、PLS第\(i\)成分までを\(X\)から引いたときの残差を表します。
PLS法では、目的変数をよく説明できるように潜在変数を取ります。 数学的には、\(w_{1}\)は \(t_{1}\)と\(y\)との共分散が最大になる ように決定します。 この条件の下で決定された\(w_{1}\)から\(t_{1}\)を計算し、線形回帰と同様の手法で\(X\)と\(y\)を\(t_{1}\)で単回帰することで\(p_{1}\)と\(q_{1}\)を決定します。 次に、A=2の場合を考えます。(1),(2)式は(6),(7)式のようになります。
\[ X = t_{1}p_{1}^{T}+t_{2}p_{2}^{T}+E_{2}-(6) \] \[ y = t_{1}q_{1}+t_{2}q_{2}+f_{1} -(7) \] ここで第1成分を左辺に移項すると、(8),(9)式を得ます。 \[ X-t_{1}p_{1}^{T} = t_{2}p_{2}^{T}+E_{2}-(8) \] \[ y-t_{1}q_{1} = t_{2}q_{2}+f_{1} -(9) \] (8),(9)式を(4),(5)式と比較すると、\(X \rightarrow X-t_{1}p_{1}^{T}; y \rightarrow y-t_{1}q_{1}\) とすれば同様のアルゴリズムで\(p_{2}\)と\(q_{2}\)を求められることが分かります。この工程を事前に決めておいた成分数Aまで行うことで回帰式を決定できます。
解析
データ作成
解析用データセットとして以下のように用意します。
import numpy as np
X1 = np.random.rand(200)*2# X1は0~2の0.01刻み
X1 = np.sort(X1)
X2 = np.random.rand(200)*10 # X2は他の変数と無相関
X3 = 5*X1 + np.random.rand(200)*1.0 # X3はX1と強い相関を持つ
X4 = 11 * np.random.rand(200) # X4は他の変数との相関はない
X4 = np.sort(X4)
y = 2*X1 + 9*X3 + X4 + np.random.rand(200)*10 # y = 2*X1 + 9*X3 + X4 + ノイズ
このように用意したXとyの図が以下になります。
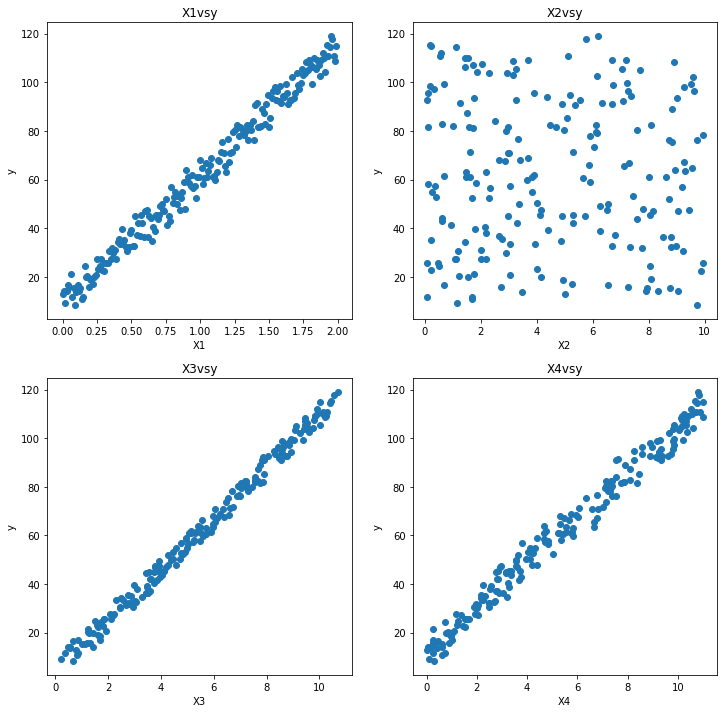
モデル構築
次に回帰モデルを構築します。
from sklearn.cross_decomposition import PLSRegression
# PLSはscikit-learnの線形回帰(Linear-Regression)のクラスに入っていないので注意!!
pls = PLSRegression(n_components=3) #PLSの成分数
上記のコードでは成分数を3に固定していますが、本来は交差検証(cross validation)等を用いて、過学習(overfitting)しないように成分数を決定します。 ここではデータ200個のうち、学習用データを100個、テストデータを100個とします。
# X1~X4までをXとします。
X1 = X1.reshape(-1,1)
X2 = X2.reshape(-1,1)
X3 = X3.reshape(-1,1)
X4 = X4.reshape(-1,1)
X = np.concatenate([X1,X2], axis=1)
X = np.concatenate([X, X3], axis=1)
X = np.concatenate([X, X4], axis=1)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5)
予測
モデルを作って予測する際に注意するべきこととして、 学習データに対して、変数の平均値を0、分散を1にする等のスケーリングを行い、同様のスケーリングをテストデータに対して行う必要がある ことが挙げられます。 スケーリングの方法は複数ありますが、スケーリングを行わないと正しい結果が得られないこともあるため注意しましょう。
from sklearn.preprocessing import StandardScaler
X_scaler = StandardScaler()
y_scaler = StandardScaler()
X_train_scaled = X_scaler.fit_transform(X_train)
y_train_scaled = y_scaler.fit_transform(y_train)
pls.fit(X_train_scaled, y_train_scaled)
X_test_scaled = X_scaler.transform(X_test)
y_pred = y_scaler.inverse_transform(pls.predict(X_test_scaled))
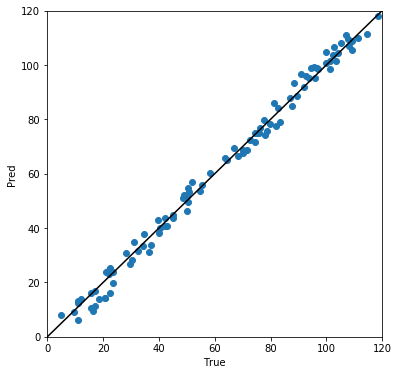
横軸を真値、縦軸を予測値としたプロットを以下に示します。 ほとんど対角線上に乗っており、真値と予測値の誤差が小さいことが確認できます。
変数の重要度
どの変数が予測に重要なのかを知りたいことはしばしばあります。 PLSモデルではモデルの標準回帰係数を求めることで、どの変数が重要であるかを判断できます。
PLSの標準回帰係数は、回帰式の項で示したP,q, wを用いて、下記のような式で定義されます。
\[ b = W(P^{T}W)^{-1}q \] 今回のケースでもこれを適応すると、以下のようなグラフが得られます。
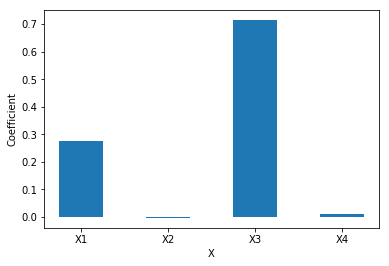
この図から\(X_{1}\), \(X_{3}\), \(X_{4}\)が重要であるということが分かり、これは、データ作成の際のyの式と合致した結果となっていることが分かります。 変数の重要性の指標として、他にもthe variable importance in projection (VIP)1等があります。
まとめ
本項では、PLS法の解説及び簡単な解析例を示しました。 また、変数の重要度の指標の一つの標準回帰係数を簡単に紹介しました。
(文責: @mtakayanagi)
-
S. Wold, PLS for multivariate linear modeling,Chemometric methods in molecular design(1995) ↩