尤度
機械学習では、尤度(ゆうど)という概念がしばしば登場します。近年流行りのBayes統計にも関連しており、今後ますますデータ解析における重要性が増してくるでしょう。しかし、その概念は一見しただけでは理解しにくいと思います。そこで、本項では尤度の定義および概念について説明します。
本項および最尤推定の項では、特に推定モデルの最適化における尤度の役割に焦点を当て例を紹介します。推定モデル構築の際、必ず何らかの指標に基づいてモデルを最適化します。しかし、その最適化の意味を理解せずに機械的にモデルを最適化すると、適切なモデルが構築できないことがあります。
そこで、本項及び最尤推定の項は「モデル最適化の際になぜ二乗誤差を最小化するのか」といったモデル構築手法を利用しているだけでは分からない疑問に答え、手法の理解を深めることを目的とします。
概要と見出し
本項では、以下の順番で説明していきます。具体例の項における回帰モデル構築には scikit-learn に実装されている linear-model[1] を用います。
定義
辞書を引いてみると、尤度とは「統計学で、もっともらしさ」[2]と書かれています。それらしい、妥当である度合いという意味合いです。これだけではまだ漠然としているので、次に数学的な定義をみてみましょう。\( N \)個の観測値\( x_{1} \), …, \( x_{N} \)が得られた時、尤度\(L\)はその値が観測される確率\( p(x_{1})\), …, \( p(x_{N})\)を用いて下式のように表されます。 (ただし、\(x_{i}\)は互いに独立であるとします) \[ L = \prod_{i=1}^N p(x_{i}) \]
一方、\(N\)回の観測によりそれぞれ観測値\( x_{1} \), …, \( x_{N} \)が得られる同時確率もまた\( \prod_{i=1}^N p(x_{i})\)となります。 このように、尤度の定義は同時確率分布のそれと全く同様です。では、何が違うのでしょうか? 次項で説明します。
同時確率分布との違い
簡潔に述べますと、同時確率分布はデータの関数であり、尤度は仮定した仮説の関数 です。 ここでの「仮説」は「得られるデータが従う法則」という意味です。
上記の観測値の例についてそれぞれの定義を言葉で書くと、以下のようになります。
・同時確率分布: ある確率分布\( p\)の下で、観測値\( x_{1} \), …, \( x_{N} \)が得られる確率
・尤度: 観測値\( x_{1} \), …, \( x_{N} \)が得られた時の、\( x \)が従うと仮定した確率分布\( p\)の尤もらしさ
それでは、実際のデータに対して尤度を計算してみましょう。
import numpy as np
from numpy import random as rd
from matplotlib import pyplot as plt
from scipy.stats import norm
# データ作成
rd.seed(7)
x = rd.randn(10,1)*0.5+5
# ベクトルxを [-5.0, ..., 5.0] の区間で作成
grid = np.linspace(-5.0, 10.0, 10000)
# 平均0, 標準偏差1の正規分布における、xの確率を求める
def normdist(x,mu,sigma):
# ndarray xに対する平均mu, 標準偏差sigmaの正規分布の確率密度関数を返す関数
return np.array([norm.pdf(x = x[i], loc = mu, scale = sigma) for i in range(len(x)) ])
# 確率密度関数、尤度の計算
p1 = normdist(grid,0,1)
p2 = normdist(grid,5,0.5)
likelihood1=np.prod(normdist(x,0,1))
likelihood2=np.prod(normdist(x,5,0.5))
# 結果のプロット
fig = plt.figure(figsize=(8, 6))
plt.plot(grid,p1)
plt.plot(grid,p2)
plt.scatter(x,np.zeros(10),color='k')
plt.text(0,norm.pdf(x=0,loc=0,scale=1)+0.05,'log(L)=%5.3f'%(np.log10(likelihood1)),ha = 'center',va = 'top', fontsize=16)
plt.text(5,norm.pdf(x=5,loc=5,scale=0.5)+0.05,'log(L)=%5.3f'%(np.log10(likelihood2)),ha = 'center',va = 'top', fontsize=16)
plt.ylim(-0.05,1)
plt.xlabel('$x$', fontsize=16)
plt.ylabel('$Probability density$', fontsize=16)
plt.legend(['(mu,sigma)=(0,1)', '(mu,sigma)=(5,0.5)','observed data'], loc='upper left', fontsize=16)
plt.tick_params(labelsize=16)
plt.show()
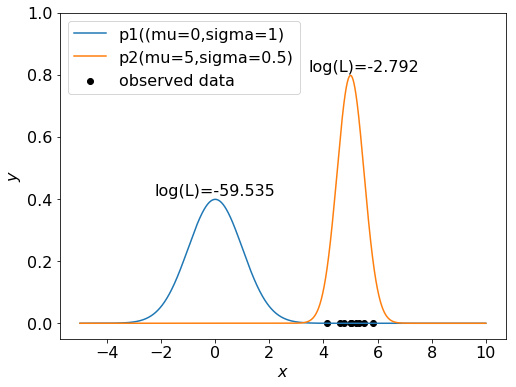
平均5,標準偏差0.5の正規分布に従うデータを10個作成し、そのデータに対して以下の2つの正規分布の尤度を計算しています。
分布1: 平均0, 標準偏差1
分布2: 平均5, 標準偏差0.5
※尤度の値は非常に小さいため、グラフ上には常用対数で示しています。
分布1(平均0,分散1)、分布2(平均5,分散0.5)に対する尤度はそれぞれ約\(10^{-59.5},10^{-2.8}\)となっています。 また同時確率分布と尤度の数学的定義は同一なので、各分布からこのデータがサンプルされる確率もこの値となります。 同時確率分布、尤度の観点からこの結果をそれぞれ解釈すると以下のようになります。
同時確率分布: このデータは、分布1より分布2からサンプルされる確率が高い。
尤度: (分布2からサンプルされる確率の方が高いため)このデータを生成した分布としては、分布1より分布2の方が尤もらしい。
同時確率分布はまずデータが従う確率分布が存在し、その条件で観測値が得られる確率を表しています。それに対し、尤度は まず観測値が存在し、その観測値の背景にある確率分布の妥当性を表しています。
上記の例では「データ\( x\)が従う確率分布を\( p\)とする」という仮説を置いていたため、尤度は\( p\)の関数となります。 この仮説として考慮できるのは、確率分布だけではありません。次項では回帰モデルのパラメタの値を仮説として、その妥当性を議論します。
具体例-回帰モデル構築
それでは、推定モデル構築における尤度の役割について解説していきます。本項では、変数\( y\)を説明変数\( x\)から推定する回帰モデル\( f\)を構築することを考えます。モデル\( f\)はパラメタ\( m\)を持つとします。つまり\( y\)の推定値\( \hat{y}\)は\( x\)と\( m\)により決まります。 \[ \hat{y}=f(x,m) \] 実際のデータにはデータ観測時の誤差など、どうしてもモデルで考慮できない不確定要素が含まれます。 このような誤差の値は予め推定できないため、ある確率分布に従う乱数と仮定するのが一般的です。 そこでモデルの誤差(モデルで考慮できない要素)\(e = \hat{y}-y\)は、確率分布\( p_{e}(e)\)に従うとします。
いま、\((x, y)\)の観測値\(\boldsymbol{d} = [(x_{1}, y_{1}); …; (x_{N}, y_{N})]\)が得られたとして、このデータ\(\boldsymbol{d}\)を基にモデルを構築します。つまり、得られたデータ\(\boldsymbol{d}\)がモデル\( f(x,m)\)に従う という仮説を考えます。
ここで、モデル\( f\)が正しく\(x, y\)の関係を表しているときに、データ\(\boldsymbol{d}\)が得られる確率\(p(\boldsymbol{d})\)を考えます。この確率が高いモデルは正しいモデルである可能性が高いといえます。 この時、回帰モデルの予測値\( f(x,m)\)と実際の\(y\)の差は、すべて上述したモデルの誤差に起因すると考えられます。 したがって、\(p(\boldsymbol{d})\)は観測値\((x_{i}, y_{i})\)に対するモデルの誤差\(e_{i}\)が\(y_{i} - f(x_{i}, m)\)に等しくなる確率であり、 \[ p(\boldsymbol{d})=\prod_{i=1}^N p_{e} (y_{i}-f(x_{i},m)) \]
となります。(各データの観測値は互いに独立としました) この確率をモデルのパラメタ\( m\)の関数として捉えたものが尤度です。 \[ L(m|\boldsymbol{d})=\prod_{i=1}^N p_{e} (y_{i}-f(x_{i},m)) \]
\((m|\boldsymbol{d})\)は、\(\boldsymbol{d}\)という条件下での\(m\)の関数 であることを表します。この場合は、\(L(m|\boldsymbol{d})\)は「データ\( \boldsymbol{d}\)が観測されたときに、モデルのパラメタが\( m\)である確率」です。この値が大きいほどパラメタ\( m\)は尤もらしく、モデルは妥当であるといえます。
それでは、以下に具体的なデータでの例を示します。今回は以下に示すデータに対して線形回帰モデルを構築します。
import numpy as np
from numpy import random as rd
from matplotlib import pyplot as plt
# データ作成
rd.seed(7)
x = rd.rand(100,1)*4-2 #-2~2の範囲の乱数を生成
y = 3*x-2 # y = 3x-2
y += rd.randn(100,1) # yに平均0, 標準偏差1の正規乱数を加算
fig = plt.figure(figsize=(8,8))
plt.scatter(x,y,marker = '+',color='k')
plt.xlabel('$x$', fontsize=16)
plt.ylabel('$y$', fontsize=16)
plt.tick_params(labelsize=14)
plt.show()
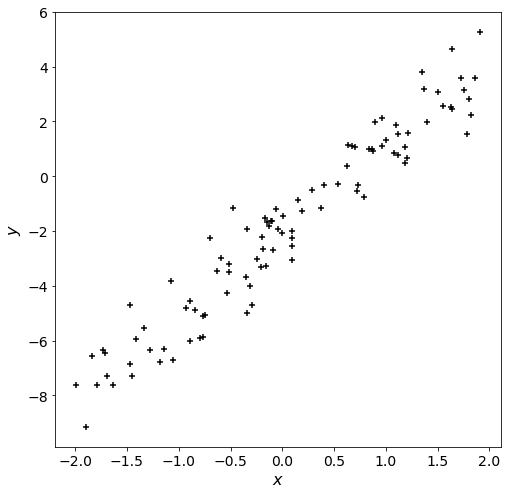
\(y\)は\(x\)の1次関数に標準正規分布(平均0, 標準偏差1の正規分布)に従うノイズを加えた変数です。そのため、尤度の計算における確率分布は標準正規分布とします。 (正規分布の確率密度関数はscipy.statsに実装されているnorm関数で計算できます)
このデータに、線形回帰モデル\(y=ax+b\)を当てはめてみます。まずは、適当に\((a, b)\)を設定してみましょう。
from scipy.stats import norm
fig = plt.figure(figsize=(8,8))
plt.scatter(x,y,marker = '+',color='k')
x_edge = np.array([min(x),max(x)])
a = np.array([1,2,3]) # 傾き
b = np.array([0,-1,-2]) # 切片
list_linestyle = ['solid','dashed','dashdot']
list_color = ['r','g','b']
L=np.zeros((3))
for i in range(3):
plt.plot(x_edge,a[i]*x_edge+b[i],color=list_color[i],linestyle=list_linestyle[i])
L[i]=np.prod(norm.pdf(x=(y-(a[i]*x+b[i])), loc=0, scale=1)) # 尤度計算
#凡例に用いる文字列を作成する関数
def make_legend(a,b):
return '(a,b)=(%d,%d)'%(a,b)
plt.legend([make_legend(a[0],b[0]),make_legend(a[1],b[1]),make_legend(a[2],b[2]),
'$Observed data$'], loc='lower right', fontsize=12)
plt.xlabel('$x$', fontsize=16)
plt.ylabel('$y$', fontsize=16)
plt.tick_params(labelsize=14)
plt.show()
# 対数尤度(尤度の常用対数)の表示
for i in range(3):
print('(a,b)=(%d,%d): logL=%03.3f'%(a[i],b[i],np.log10(L[i])))
# (a,b)=(1,0): logL=-238.974
# (a,b)=(2,-1): logL=-104.802
# (a,b)=(3,-2): logL=-57.672
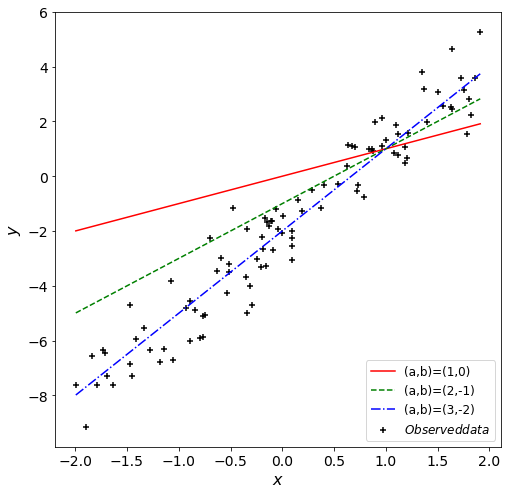
グラフを見る限り、\((a,b)=(3,-2)\)が最も合っていそうですね。尤度も最も大きいです。
(尤度の値は約\(2\times10^{-58}\)と小さいですが、この値は「100個のデータが丁度特定の値になる確率」という意味を持つため、妥当な値といえます)
本データは\(y=3x-2\)に乱数を足して作成したため、妥当な結果が得られたといえます。
では、本当に\((a, b)=(3,-2)\)が最も適切なパラメタなのでしょうか? 今度はscikit-learnの関数を用いてモデルを構築してみます。
from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(x,y) #モデル構築
ypred = model.predict(x) #予測値計算
L_LinearRegression=np.prod(norm.pdf(x=y-ypred, loc=0, scale=1)) # 尤度計算
print("y={0:.5f}x{1:+.5f}".format(model.coef_[0][0],model.intercept_[0])) #回帰式の表示
# y = 3.07553x - 2.00268
plt.scatter(x,y,marker = '+',color='k')
plt.plot(x,model.predict(x),color='r')
plt.xlabel('$x$', fontsize=16)
plt.ylabel('$y$', fontsize=16)
plt.tick_params(labelsize=14)
plt.show()
print("log(L_LinearRegression)={0:.3f}".format(np.log10(L_LinearRegression)))
# log(L_LinearRegression)=-57.533
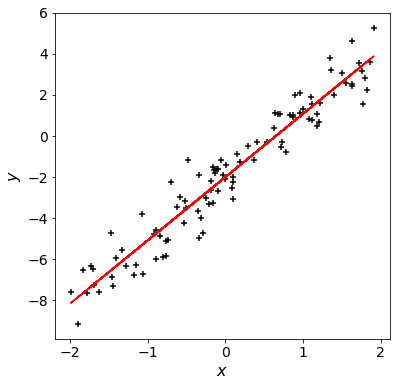
\((a,b)=(3,-2)\)に比べわずかに尤度が向上しました。加えたノイズの影響で、最適な回帰式にずれが生じたことが分かります。
linear-modelは最小二乗法[3]に基づいて線形回帰モデルを構築していますが、実は今回の例では最小二乗法によるモデルが最も尤度の高いモデルを構築できます。 このように、尤度を最大化することでモデルのパラメタを決定する手法が最尤推定法です。
ただし、いつでも最小二乗法によるモデルが最も尤度が高くなるわけではありません。 最尤推定に関しては、別の記事で詳述します。
まとめ
本項では尤度の定義を解説し、回帰分析における尤度とモデルの妥当性について例示しました。尤度は少々分かりにくい概念ですが、本項がその理解の一助になれば幸いです。
参考文献
scikit-learn 0.19.1 documentation
(文責: @tawatanabe)